publications

2025

1. 

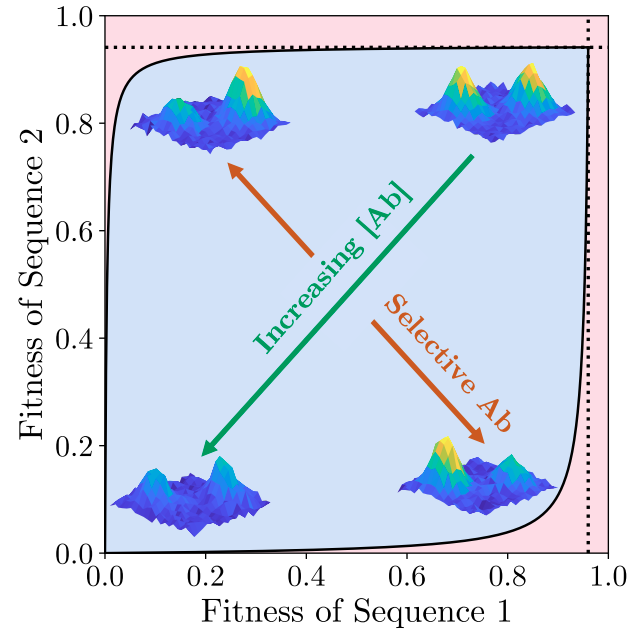   Phase diagrams for biophysical fitness landscape design

   Vaibhav Mohanty and Eugene Shakhnovich

   bioRxiv:2025.09.10.675274, 2025

   Abs DOI

   Populations evolve toward the top of fitness landscapes in the way that physical particles experience forces toward the bottom of a potential energy landscape. We recently introduced fitness landscape design (FLD) as a means of customizing the shape of a protein’s biophysical fitness landscape by using antibody sequences and concentrations as tunable control parameters. Until now, previous evidence for the feasibility of FLD has been numerical and simulated. Here, we derive an explicit analytical theory for the FLD phase diagram, providing tight bounds on the designability frontiers describing the extent to which fitnesses of different protein sequences can be tuned independently of each other. We then leverage a recently published experimental dataset of binding affinities between over 62,000 antibody variants and each of three glycoprotein antigens to construct experimental FLD phase diagrams, which show close agreement with theory. These results support the feasibility of engineering quantitatively programmable fitness landscapes for laboratory protein evolution experiments.

2. 

   Biophysical fitness landscape design traps viral evolution

   Vaibhav Mohanty and Eugene I. Shakhnovich

   bioRxiv:2025.03.30.646233, 2025

   Abs DOI

   Evolutionary adaptation is often visualized as a population’s stochastic climb toward the top of a fitness landscape. While there exist approaches to design or synthetically evolve proteins into desired structures, there is a lack of methodology for designing, tuning, and quantitatively reshaping the fitness landscapes themselves on which protein evolution takes place. Here, we introduce foundational principles of fitness landscape design (FLD) to customize the structural peaks and valleys of biophysical fitness landscapes with quantitative accuracy, offering robust control of long-term evolutionary outcomes. Our FLD algorithms use stochastic optimization of a chemically derived biophysical fitness model to consistently discover optimal antibody ensembles which force a target protein to evolve according to a user-specified target fitness landscape. We then apply FLD to suppress the fitnesses of two SARS-CoV-2 genotype neutral networks and to discover proactive vaccines that preemptively restrict escape variant fitness trajectories before they arise.

3. 

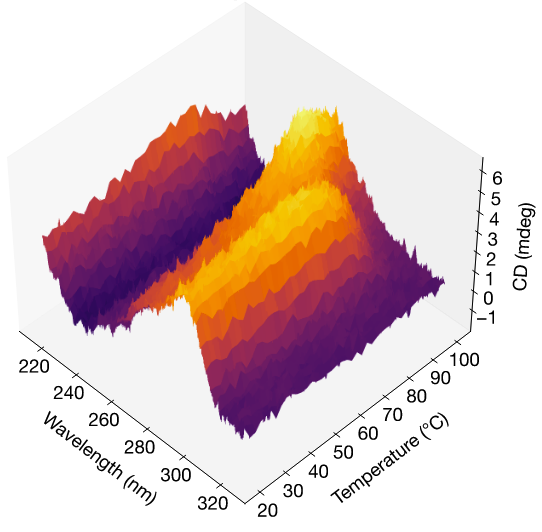   Thermally activated irreversible homogenization of G-quadruplexes in an ALS/FTD-associated nucleotide expansion

   Daniel Ross, Olivia Lewis, Olivia McLean, Sundeep Bhanot, Shane Donahue, Rachael Baker, Randi Dias, David Eagerton, Vaibhav Mohanty, and Bidyut K. Mohanty

   bioRxiv:2025.06.02.657482, 2025

   Abs DOI

   A significant proportion of familial amyotrophic lateral sclerosis (ALS) and frontotemporal dementia (FTD) cases exhibit a substantial copy number expansion of the hexanucleotide GGGGCC/GGCCCC sequence in the C9ORF72 gene. The GGGGCC sequence forms a non-canonical DNA structure called a G-quadruplex (G4) which has been associated with the disease states and with nucleic acid condensate formation, but there remains poor understanding of why the hexanucleotide repeat expansion occurs. An important clue may lie in the thermodynamic properties of various G4 configurations. Here, we use temperature-swept CD spectroscopy to observe configurational homogenization of an initially heterogeneous population of G4s over a small range of temperatures, demonstrating phase transition-like behavior. We further show that this reaction is irreversible, suggesting that the metastable non-parallel G4s are trapped over long timescales by a transition state barrier; upon heating, the relative height of the free energy barrier is lowered, and a thermally activated metastable-to-stable transition to parallel G4s rapidly occurs. We provide an analytical theory based on a two-state thermodynamic model which offers mechanistic insight into the experimental evidence. These findings suggest that kinetic regulation of non-canonical DNA structures may play a role in cellular homeostasis or disease pathogenesis.

4. 

   Probabilistic genotype-phenotype maps reveal mutational robustness of RNA folding, spin glasses, and quantum circuits

   Anna Sappington and Vaibhav Mohanty

   Physical Review Research, 2025

   Abs DOI

   Recent studies of genotype-phenotype maps have reported universally enhanced phenotypic robustness to genotype mutations, a feature essential to evolution. Virtually all of these studies make a simplifying assumption that each genotype—represented as a sequence—maps deterministically to a single phenotype, such as a discrete structure. Here we introduce probabilistic genotype-phenotype (PrGP) maps, where each genotype maps to a vector of phenotype probabilities, as a more realistic and universal language for investigating robustness in a variety of physical, biological, and computational systems. We study three model systems to show that PrGP maps offer a generalized framework which can handle uncertainty emerging from various physical sources: (1) thermal fluctuation in RNA folding, (2) external field disorder in the spin-glass ground state search problem, and (3) superposition and entanglement in quantum circuits, which are realized experimentally on IBM quantum computers. In all three cases, we observe a biphasic robustness scaling which is enhanced relative to random expectation for more frequent phenotypes and approaches random expectation for less frequent phenotypes. We derive an analytical theory for the behavior of PrGP robustness, and we demonstrate that the theory is highly predictive of empirical robustness.

2024

1. 

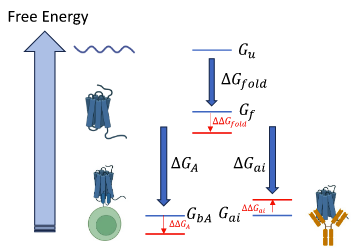   Biophysical principles predict fitness of SARS-CoV-2 variants

   Dianzhuo Wang, Marian Huot, Vaibhav Mohanty, and Eugene I. Shakhnovich

   Proceedings of the National Academy of Sciences, 2024

   Abs DOI

   SARS-CoV-2 employs its spike protein’s receptor binding domain (RBD) to enter host cells. The RBD is constantly subjected to immune responses, while requiring efficient binding to host cell receptors for successful infection. However, our understanding of how RBD’s biophysical properties contribute to SARS-CoV-2’s epidemiological fitness remains largely incomplete. Through a comprehensive approach, comprising large-scale sequence analysis of SARS-CoV-2 variants and the identification of a fitness function based on binding thermodynamics, we unravel the relationship between the biophysical properties of RBD variants and their contribution to viral fitness. We developed a biophysical model that uses statistical mechanics to map the molecular phenotype space, characterized by dissociation constants of RBD to ACE2, LY-CoV016, LY-CoV555, REGN10987, and S309, onto an epistatic fitness landscape. We validate our findings through experimentally measured and machine learning (ML) estimated binding affinities, coupled with infectivity data derived from population-level sequencing. Our analysis reveals that this model effectively predicts the fitness of novel RBD variants and can account for the epistatic interactions among mutations, including explaining the later reversal of Q493R. Our study sheds light on the impact of specific mutations on viral fitness and delivers a tool for predicting the future epidemiological trajectory of previously unseen or emerging low-frequency variants. These insights offer not only greater understanding of viral evolution but also potentially aid in guiding public health decisions in the battle against COVID-19 and future pandemics.

2023

1. 

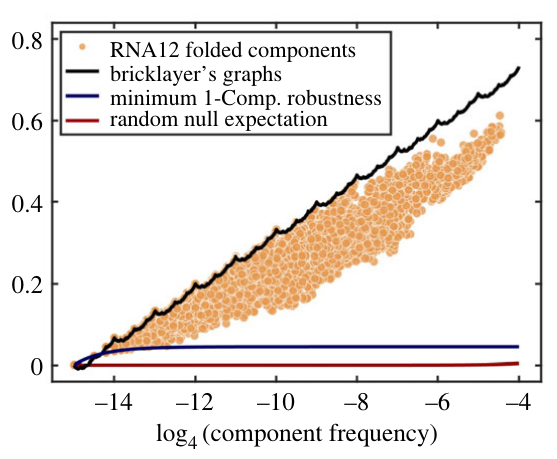   Maximum mutational robustness in genotype–phenotype maps follows a self-similar blancmange-like curve

   Vaibhav Mohanty, Sam F. Greenbury, Tasmin Sarkany, Shyam Narayanan, Kamaludin Dingle, Sebastian E. Ahnert, and Ard A. Louis

   Journal of The Royal Society Interface, 2023

   Abs DOI

   Phenotype robustness, defined as the average mutational robustness of all the genotypes that map to a given phenotype, plays a key role in facilitating neutral exploration of novel phenotypic variation by an evolving population. By applying results from coding theory, we prove that the maximum phenotype robustness occurs when genotypes are organized as bricklayer’s graphs, so-called because they resemble the way in which a bricklayer would fill in a Hamming graph. The value of the maximal robustness is given by a fractal continuous everywhere but differentiable nowhere sums-of-digits function from number theory. Interestingly, genotype–phenotype maps for RNA secondary structure and the hydrophobic-polar (HP) model for protein folding can exhibit phenotype robustness that exactly attains this upper bound. By exploiting properties of the sums-of-digits function, we prove a lower bound on the deviation of the maximum robustness of phenotypes with multiple neutral components from the bricklayer’s graph bound, and show that RNA secondary structure phenotypes obey this bound. Finally, we show how robustness changes when phenotypes are coarse-grained and derive a formula and associated bounds for the transition probabilities between such phenotypes.

2. 

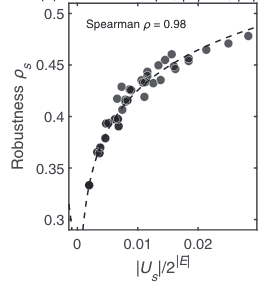   Robustness and stability of spin-glass ground states to perturbed interactions

   Vaibhav Mohanty and Ard A. Louis

   Physical Review E, 2023

   Abs DOI

   Across many problems in science and engineering, it is important to consider how much the output of a given system changes due to perturbations of the input. Here, we investigate the glassy phase of ±J spin glasses at zero temperature by calculating the robustness of the ground states to flips in the sign of single interactions. For random graphs and the Sherrington-Kirkpatrick model, we find relatively large sets of bond configurations that generate the same ground state. These sets can themselves be analyzed as subgraphs of the interaction domain, and we compute many of their topological properties. In particular, we find that the robustness, equivalent to the average degree, of these subgraphs is much higher than one would expect from a random model. Most notably, it scales in the same logarithmic way with the size of the subgraph as has been found in genotype-phenotype maps for RNA secondary structure folding, protein quaternary structure, gene regulatory networks, as well as for models for genetic programming. The similarity between these disparate systems suggests that this scaling may have a more universal origin.

2020

1. 

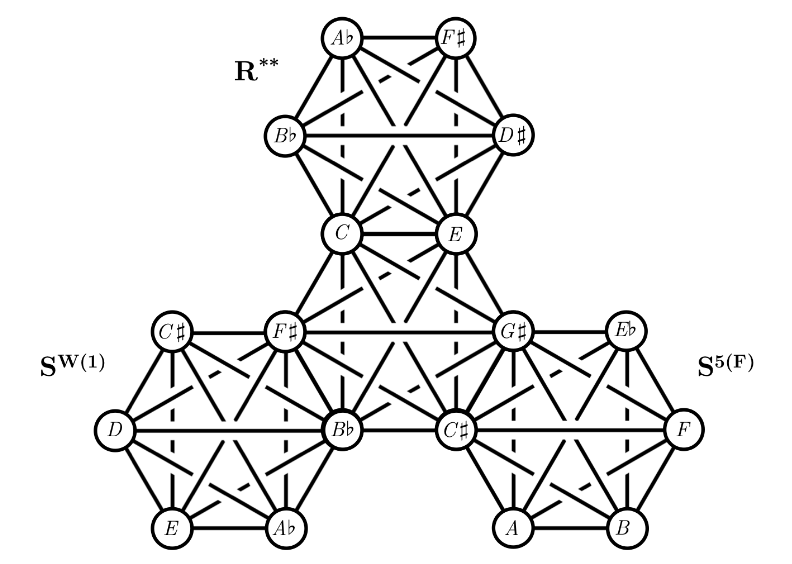   A 5-dimensional Tonnetz for nearly symmetric hexachords

   Vaibhav Mohanty

   Journal of Mathematics and Music, 2020

   Abs DOI

   The standard 2-dimensional Tonnetz describes parsimonious voice leading connections between major and minor triads as the 3-dimensional Tonnetz does for dominant seventh and half-diminished seventh chords. In this paper, a 5-dimensional Tonnetz is introduced, providing a geometric framework for parsimonious voice leading among nearly symmetric hexachords of the mystic-Wozzeck genus. Cartesian coordinates for points on this discretized grid, generalized coordinate collections for the vertices of the 5-simplices corresponding to mystic and Wozzeck chords, and the geometric nearest-neighbours of a selected chord are derived.

2019

1. 

   Lazy electrons in graphene

   Vaibhav Mohanty and Eric J. Heller

   Proceedings of the National Academy of Sciences, 2019

   Abs DOI

   Within a tight-binding approximation, we numerically determine the time evolution of graphene electronic states in the presence of classically vibrating nuclei. There is no reliance on the Born–Oppenheimer approximation within the p-orbital tight-binding basis, although our approximation is “atomically adiabatic”: the basis p-orbitals are taken to follow nuclear positions. Our calculations show that the strict adiabatic Born–Oppenheimer approximation fails badly. We find that a diabatic (lazy electrons responding weakly to nuclear distortions) Born–Oppenheimer model provides a much more accurate picture and suggests a generalized many-body Bloch orbital-nuclear basis set for describing electron–phonon interactions in graphene.

2018

1. 

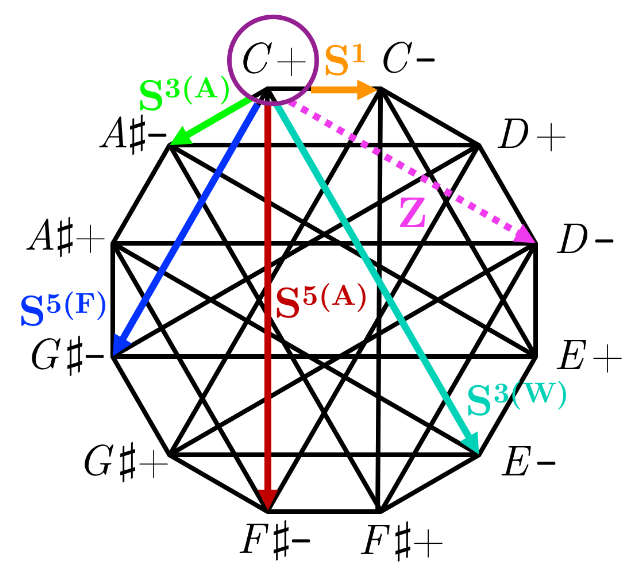   Dodecatonic Cycles and Parsimonious Voice-Leading in the Mystic-Wozzeck Genus

   Vaibhav Mohanty

   arXiv:1805.11087, 2018

   Abs DOI

   This paper develops a unified voice-leading model for the genus of mystic and Wozzeck chords. These voice-leading regions are constructed by perturbing symmetric partitions of the octave, and new Neo-Riemannian transformations between nearly symmetric hexachords are defined. The behaviors of these transformations are shown within visual representations of the voice-leading regions for the mystic-Wozzeck genus.

2. 

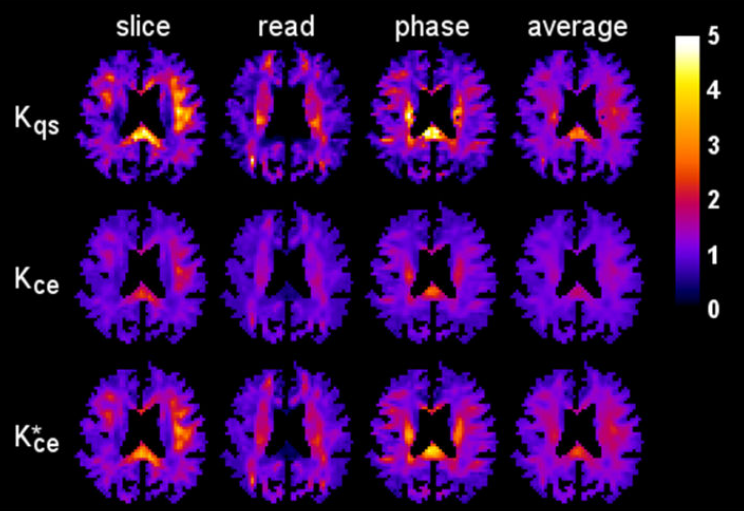   Comparison of cumulant expansion and q-space imaging estimates for diffusional kurtosis in brain

   Vaibhav Mohanty, Emilie T. McKinnon, Joseph A. Helpern, and Jens H. Jensen

   Magnetic Resonance Imaging, 2018

   Abs DOI

   Purpose To compare estimates for the diffusional kurtosis in brain as obtained from a cumulant expansion (CE) of the diffusion MRI (dMRI) signal and from q-space (QS) imaging. Theory and methods For the CE estimates of the kurtosis, the CE was truncated to quadratic order in the b-value and fit to the dMRI signal for b-values from 0 up to 2000s/mm2. For the QS estimates, b-values ranging from 0 up to 10,000s/mm2 were used to determine the diffusion displacement probability density function (dPDF) via Stejskal’s formula. The kurtosis was then calculated directly from the second and fourth order moments of the dPDF. These two approximations were studied for in vivo human data obtained on a 3T MRI scanner using three orthogonal diffusion encoding directions. Results The whole brain mean values for the CE and QS kurtosis estimates differed by 16% or less in each of the considered diffusion encoding directions, and the Pearson correlation coefficients all exceeded 0.85. Nonetheless, there were large discrepancies in many voxels, particularly those with either very high or very low kurtoses relative to the mean values. Conclusion Estimates of the diffusional kurtosis in brain obtained using CE and QS approximations are strongly correlated, suggesting that they encode similar information. However, for the choice of b-values employed here, there may be substantial differences, depending on the properties of the diffusion microenvironment in each voxel.